COMPOUND INTERE$T.

1. The annual interest rate.

2. How often interest is compounded.

We have already seen two examples of compounded interest, although in those Jane had to do the compounding herself. As another example, suppose you deposit $1000 at 5% for a period of 2 years and that it is compounded every 6 months. Then the interest paid at the end of each six month period is one-half of 5% of the balance at the beginning of the period. This reflects the fact that 5% is an annual interest rate and six months is one-half of a year. Here is what happens to your balance:

Elapsed Time	Beginning Account Balance	Interest Paid	Ending Account Balance
6 months	$1000	1/2 .05 $1000 = $25	$1025
12 months	$1025	1/2 .05 $1025 = $25.62	$1050.62
18 months	$1050.62	1/2 .05 $1050.62 = $26.27	$1076.89
24 months	$1076.89	1/2 .05 $1076.89 = $26.92	$1103.81

At the end of 2 years you have $1103.81. Had your interest not been compounded, you would have had only $1000 plus 2 5% $1000 which is $1100, so you came out $3.81 ahead.

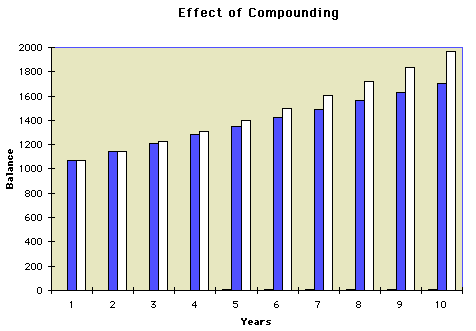
Financial advisors and books on personal finance often point out the "miracle" of compound interest. This "miracle" is one that takes place over longer periods of time. For example, if you invest your money at a 7% interest rate and simply compound the interest earned once per year, after 10 years instead of having earned interest worth 70% of your original principal, you have earned interest worth 96.71% of your original principal.

Suppose we start with a balance of B dollars and we receive 5% interest compounded every 6 months. This is exactly the situation in the example above, with B = 1000. Then at the end of 6 months the balance (in dollars) will be

	5%
B [the original balance] +		[half of the interest rate] B [the original balance].
	2

Factoring out B, this can be expressed as

(1 + 5%/2) B or (1 + .05/2) B or (1.025) B

The neat thing about this formula is that it represents the new balance after any 6-month period during which 5% interest is paid. So to see how much is in the bank after one year, we can think of the year as being comprised of two 6-month chunks. 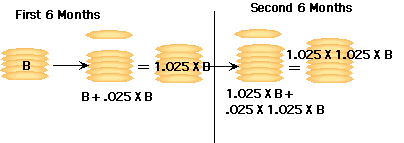If we deposit B dollars at an annual interest rate of 5% compounded every 6 months, then after 6 months the balance is 1.025 B dollars, and after one year the balance is 1.025 this balance, or 1.025 1.025 B dollars. If we leave the money in the bank for another year, which consists of another two 6 month periods, then the ending balance becomes 1.025 1.025 1.025 1.025 B dollars, or (1.025)⁴ B dollars.

• we are given an interest rate of r% per year and
• we compound the interest n times per year.

Then the year is divided into n equal time periods during which we earn r/n percent interest. If you start one of these time periods with a balance of B dollars, you will end it with a balance of

(1 + r/n) B

dollars, so if you leave your money in the bank for one year, your balance will grow to (1 + r/n)ⁿ B dollars. If you leave the same money in for y years, then the number of compounding periods is n y, so

If you deposit B dollars for y years at an interest rate of r compounded n times per year, then your ending balance is (1 + r/n)(y n) times B dollars.

Example. Suppose you deposit $1000 in a bank which pays 5% interest compounded daily, meaning 365 times per year. How much more do you earn as opposed to simple interest of 5% if you leave your money in the bank for 1 year? For 5 years?

Solution. Referring to the formula above, the interest rate r is 5% or .05 and the number of equal time periods, n, is 365. Thus at the end of 1 year your balance is (1 + .05/365)³⁶⁵ $1000, or (using a calculator) $1051.27. The interest you earned is $51.27. Simple interest would have paid $50 in interest, so you earn $1.27 more.

If you leave the money in the bank for 5 years, then the formula becomes (1 + .05/365)^{5 365} $1000, which works out to be $1284. This means you received $284 in interest. Simple interest would have paid .05 5 $1000 = $250 in interest, so your gain is $34.

Try it yourself!

You will be best off using your own calculator for this, but we have supplied a clumsy one which you can use as an aid. To use it, type numbers into the first two slots, select an operation (addition (+), multiplication (X), division (/), or raising to a power (^)) and click on the "equals" button. You can cut and paste results into the first two slots as needed.

Select Interest Rate	Select Years	Select Compounding Frequency	Enter Value
2% 3% 4% 5% 6%	1 year 2 years 3 years 4 years 5 years	once per year twice per year 4 times per year 12 times per year 365 times per years	What is the ending balance if $1000 is deposited for the selected number of years at the selected rate compounded as selected? $

+ x / ^

CLEAR

© 1997,1998 Robby Robson, Oregon State University.